Poker Hand Rankings And Odds
Find all poker hands ranked from best to worst. Use the OFFICIAL poker hand rankings to know what beats what in poker. Download the PDF list of poker hands.
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
- Dec 21, 2020 The poker hand rankings dictate that a straight is a stronger hand than two pair. The straight occurs with about 21-to-1 odds against in Texas Hold’em, while the odds against making two pair stand at about 3-to-1.
- Omaha Odds and Starting Hand Ranking for All Starting Hands. There are 270725 different combinations possible. Odds for 7 different categories.
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
High Card
The count is the complement that makes up 2,598,960.
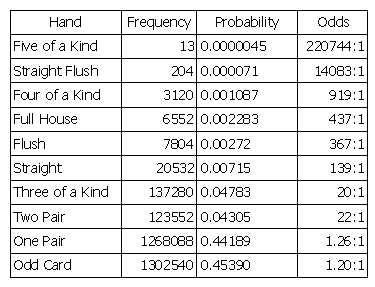
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
___________________________________________________________________________
2017 – Dan Ma
Poker is a very technical casino game and you can easily be overwhelmed if you are just starting out. There are different variations of online poker games each with slightly different rules.
However, the ten different types of hands you can make are constant.
Finding an easy way for a beginner to learn these hands will help you get started quickly. With this poker hand cheat sheet, you’ll get an overview of all the poker hands you can make.
While there will be slight variations as you play different poker games, this should not deter you from getting started with the basics.
Highest value hands in Poker – the Flushes
Each hand in poker is made up of five cards. Depending on the game variant, players can make that hand from different numbers of their own and community cards.
Poker hands are ranked in value and the rules that govern the content of each hand are the same:
- The highest value hand is the Royal Flush – a straight run of five cards with values from 10 to Ace all in the same suit.
- Straight Flush is the next highest – all cards are from the same suit and run sequentially, e.g. 6 to 10 of spades or 9 to K of diamonds.
Middle value hands in poker
After the Flushes, there are several other hands that you can form to hit a win in poker. In order of value, they are:
- Four of a Kind – which involves four cards of the same rank but different suits.
- A Full House – which is a combination of three of a kind and a pair.
- A Flush – five cards from the same suit, not in any sequence.
- A Straight – five cards in a sequence, but not from the same suit.
- Three of a Kind – three cards with the same rank, but from different suits.
Lowest value hands in poker
The last three poker hands are the lowest-ranked and are:
- Two pair – Two different pairs with all cards being from any suit.
- Pair – two cards of the same rank but different suits.
- High card – This is only used when you have not made any of the hands previously described.
In this case, the highest card in your hand is played. One other point to remember is that if you play the same hand as the dealer, the value of the cards within that hand determines the winner.
For example, if both have four-of-a-kind, then four kings would win over four sixes.
Poker hand odds
To successfully apply what you have learnt, you need to understand the odds of different hands in various poker games.
Generally, poker hands are played with 5 cards, however, there are some variants that use 7 cards. These games have higher odds for making specific hands compared to 5-card poker, although not in all cases.
For a Royal flush, a 5-card poker game has odds of this occurring of 0.00015% compared to 0.0032% in a 7-card poker game.
However, the odds of getting a high card are 50.1% in a 5-card poker game compared to 17.4% in 7-card poker.
Using Poker tools

There are different forms of poker tools you can use to improve your skill. The most popular type is the poker simulator.
This tool mimics a real poker round, however, you will be playing against a computerized dealer.
The good thing is that it is free. Another poker tool is the Propoker tool. This is an equity calculator for various versions of poker games.
If you want a tool made for beginners, you can check out the Hold’em Poker trainer. This simple tool provides you with free online exercises to practice ranking hands, making the best hand, and more.
Poker Hand Cheat Sheet Conclusion
This poker hand cheat sheet is going to be helpful when playing in the real world of poker but there is one other important thing to bear in mind. That is positional play, which relates to your position at the table in relation to the dealer.

The three positions are termed early, middle, and late.
The early position is usually considered to be the first three seats to the left of the dealer and is considered weak. The middle position is considered better since it offers the opportunity to play based on what the early position players have. The late position is the strongest as you’ll have seen all other players’ actions.
However, when playing poker online, you play against the dealer only, regardless of whether you are playing virtual or live poker games.
For beginners, having a good grasp of the different poker hands and their respective rankings will stand you in good stead. This is where our poker hand cheat sheet will come in handy and help you get ahead.
Of course, the more you play the more familiar you’ll become with the different hands. Then you can test out your skill for free using some of the online poker tools available, before playing for real money at your favorite casino site.
FAQs
How do you score hands in poker?The top 10 hands:
1. Royal flush – A, K, Q, J, 10, all the same suit.
2. Straight flush – Five sequenced cards in the same suit.
3. Four of a kind – Four cards with the same rank.
4. Full house – Any three of a kind with a pair.
5. Flush – Five cards with the same suit that’s not in a sequence.
6. Straight – Five sequenced cards that’s not of the same suit.
7. Three of a kind – Any three cards with the same rank.
8. Two pair – Two pairs of different ranks and suits.
9. Pair – Two cards with the same rank.
10. High Card – None of the above but you have the highest card.
It’s an Ace-High Royal Flush or Ace, King, Queen, Jack, Ten with the same suit.
What hands should you always play in poker?Poker Hand Rankings And Odds College Football
Any big pocket pair, high cards like Ace, King, Queen, and Jack. Always play big-suited connectors and big-connectors off suit.